グラフの計測

グラフを拡大して計測バーによる計測を行います

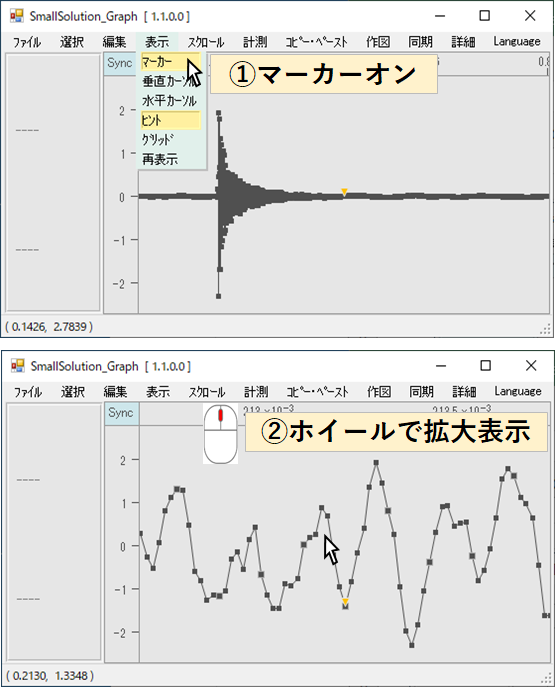
①「表示」→「マーカー」をオンにします

②ホイールで１つ１つのマーカーが見えるところまで拡大します

③「計測」→すべてのバーをオンにします

④水平バーはグラフ選択すれば表示されます

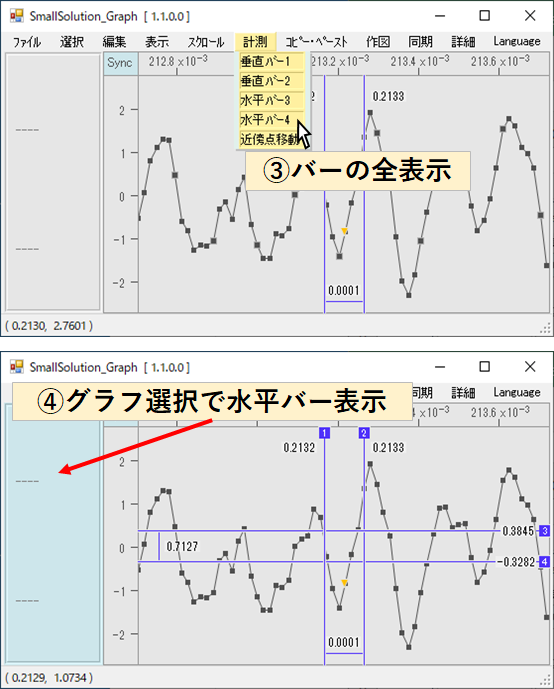
バーの位置とバー間の計測値が表示されます。次にバーの番号部分をつまんで任意の位置に移動させます

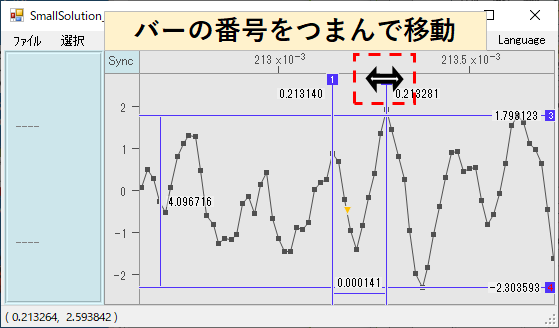
バーはプロット点に近づくと吸付かれるように移動します

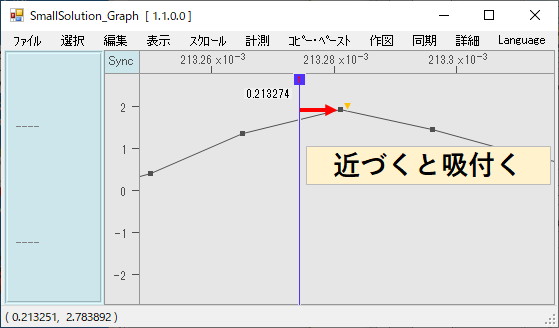
吸付かない場合は

・「計測」→「近傍点移動」のオンを確認し、

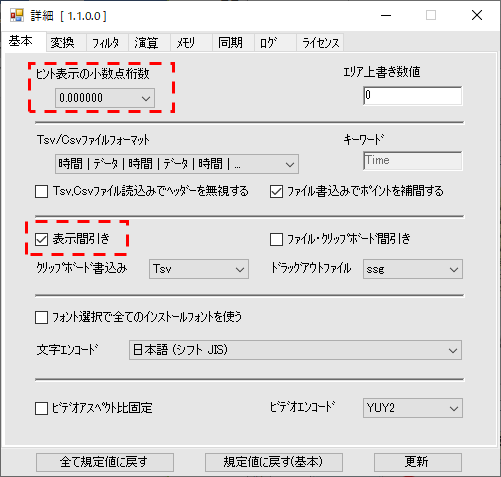
・「詳細」→基本タブの「表示間引き」のオンを確認てください

両オンでないと近傍点移動はしません

また、計測に関わる設定で「詳細」→基本タブの「ヒント表示の小数点桁数」で、バー表示の桁数を変更できます

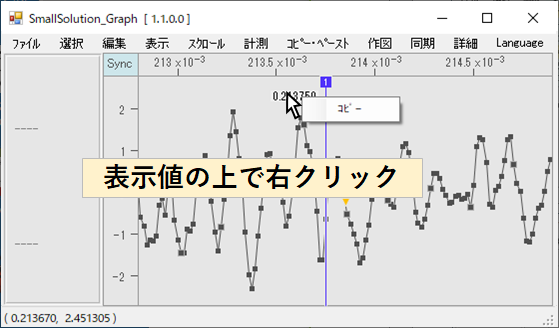
グラフ計測値のコピー

バーの表示値上でマウス右クリックすると、その値をコピーできます

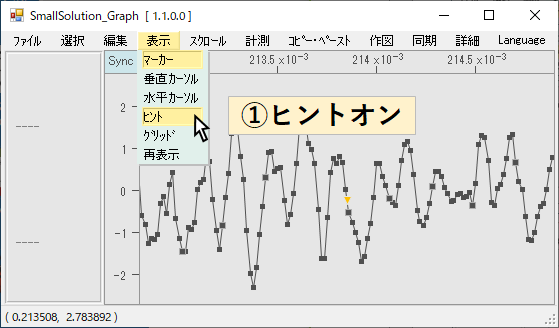
・「表示」→「ヒント」のオンを確認します

・マウスをマーカー上にのせると、その点の座標値が表示されます

・マウス右クリックで、その座標値をコピーできます

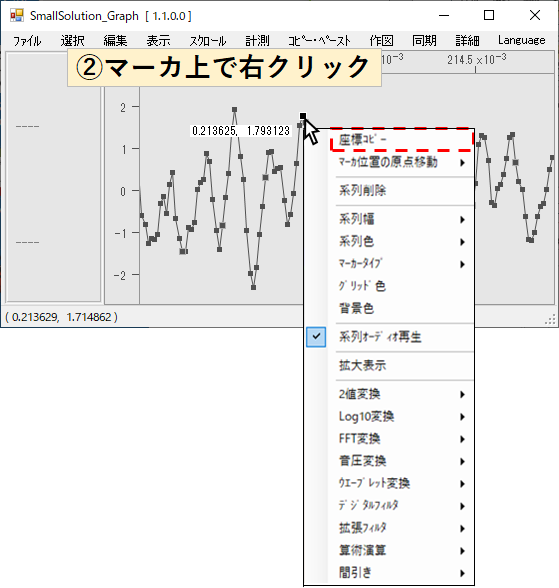
グラフの分析・・・音圧変換、ウェーブレット変換

分析手法の１つとして、音のレベルだったり、どの周波数が発生しているかなどを音圧変換やウェーブレット変換でみることができます。その事例を以下の手順で説明します

・まず説明のため「Can.csv」を３回読込みます

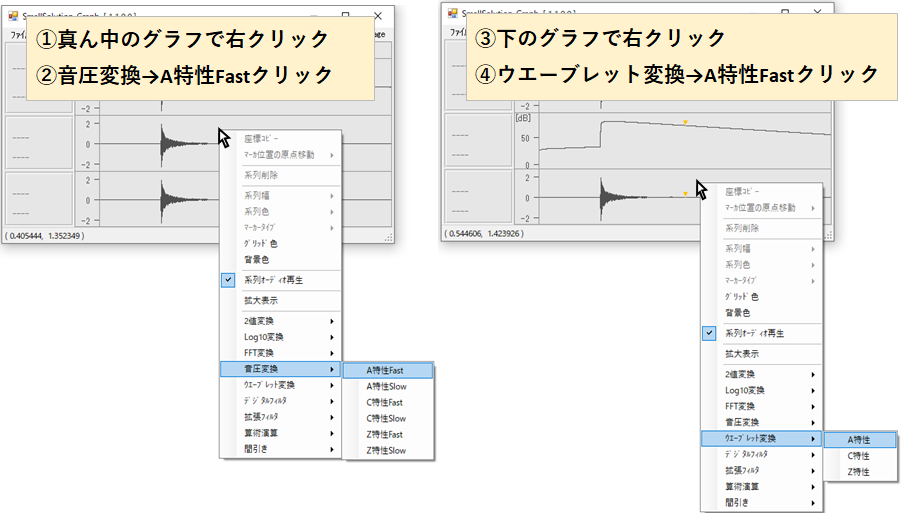
・①真ん中のグラフで右クリックして②「音圧変換」→「A特性Fast」をクリックすると、音圧変化のグラフが現れます

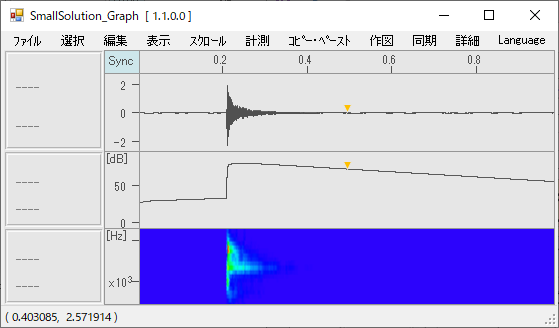
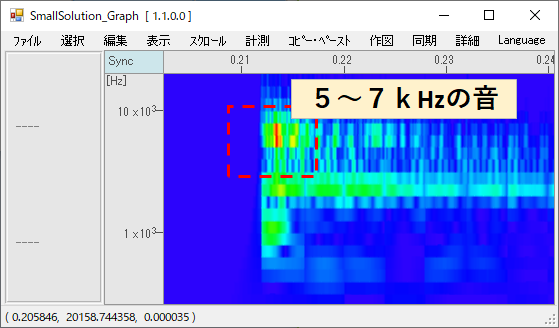
・③一番下のグラフで右クリックして④「ウェーブレット変換」→「A特性Fast」をクリックすると、どの時間でどの周波数の音が発しているかわかります

グラフの分析・・・正弦波PWM波形

DCモータを駆動させるときに電圧をPWM駆動させることはよくあります。その駆動を正弦波でおこなうときに出力されるPWM波形のDutyを求めグラフ化してみます

・①テストデータの「SinPwm.csv」を読込みます

・③グラフ上で右クリックして④「２値変換」→「Dutyハイ」をクリックすると疑似的な正弦波形が現れます

グラフの分析・・・速度パルス波形

ステッピングモータを駆動させるときに駆動パルスをステッピングモータに与えます。その駆動パルスはモータが脱調しないように台形速度で与えることはよくあります。その駆動パルスを周波数変換してどのような速度波形になっているかグラフ化してみます

・①テストデータの「MotPulse.csv」を読込みます

・③グラフ上で右クリックして④「２値変換」→「周波数ハイエッジ」をクリックすると加速時の速度波形が現れます。縦軸は周波数で表記してますが、実際には[pulse/sec]となります

グラフの分析・・・ロト６

ここまでの分析は純技術的な話でしたが、最近ロト６も分析したので報告します

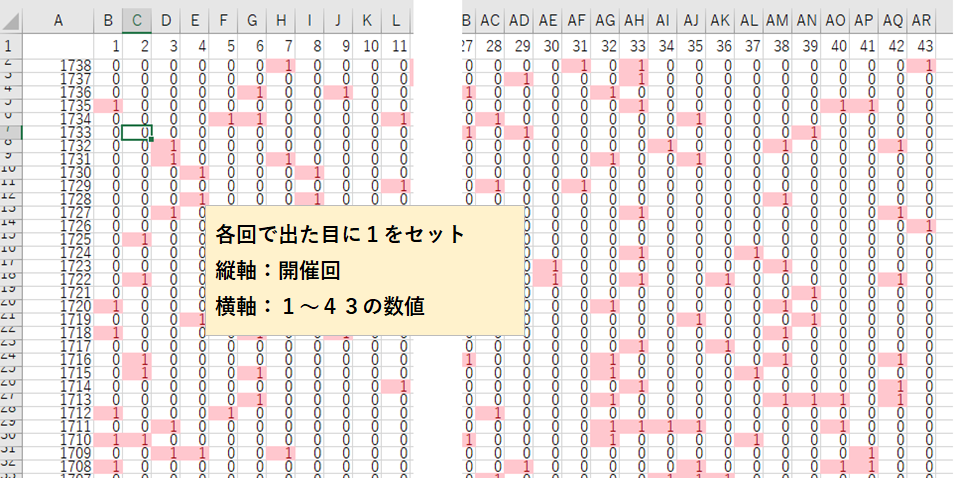
まずエクセルで、各回での出目を出た場合に１としデータ化します。一度作ってしまえば、あとはデータを追加するだけなのですが、一回作り上げるまではちょっと面倒です

以降でいくつかの変換処理を行いますが、一括で変換させた方がいいので以下の設定をします

①詳細パネルの変換タグ「選択グラフの一括変換」にチェックを入れます

②「更新」をクリックして抜けます

ここからデータを読んでグラフ化してきます

①テストデータ「ﾛﾄ6.xlsxのsheet2」をコピペで読込みます。①から③までのグラフはデータは見やすくするため、あえて４ケのデータを読み込んだ例となっていて、更に見やすくするために拡大してます

②「選択」→「全選択」をクリックして全てのグラフを選択します

④グラフ上で右クリックして「算術演算」→「Y値積算」をクリックするとY値を１つ１つを加算してグラフ化します。これがロト６出目の累積グラフです

④数字1～43のロト６の出目の累積を示します

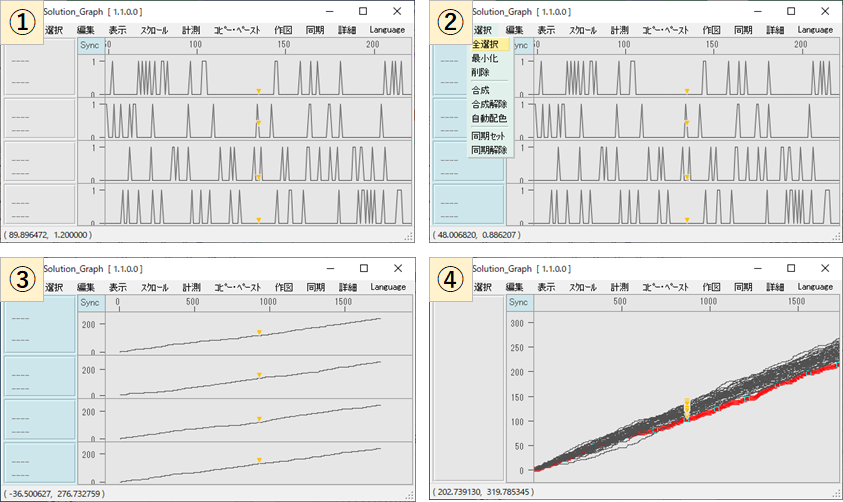
この時点でロト６回数は１７００回を超えていたので、出目は理論値（各グラフの真ん中）に近づいているかと思ってたのとは違い結構分散してるなって感想を持ちました。また、９の出目のグラフを赤くしてますが、出目がいつ理論値に近づくような動きをするんだろう？確率論を否定するわけではないのですが、確率って本当に同じになっていくのかなという感想も持ちました
結局、ロト６でよくでる数字は、次も出るのか→いやいや出すぎてるのだからでる確率は低い？出てない数値は次は出やすいのか→いやいや確率が低いのだから次もでない？
結局迷路の中からでることはできない状態ですが、適当に選ぶよりは面白いです

詳細パネルの変換タグ「選択グラフの一括変換」はチェックをオフにしておいてください

直線フィッティング

エクセルの直線フィッティングはグラフ全体でとらえてしますので、一部の傾きを見たくても融通が利かなかったり、見た目で「ちょっと違うな」みたいな所に近似します。これはこれでいいのですが、概略でもいいのでもっと簡単手軽に近似したいという思いで手動フィッティングを作りました
直線は移動したり端点をつまむと自由に傾きを変更できるので、グラフに合わせて移動と変形させて手動でフィッティングします

①「作図」→「直線フィッティング」をクリック

②グラフに沿って直線を引きます

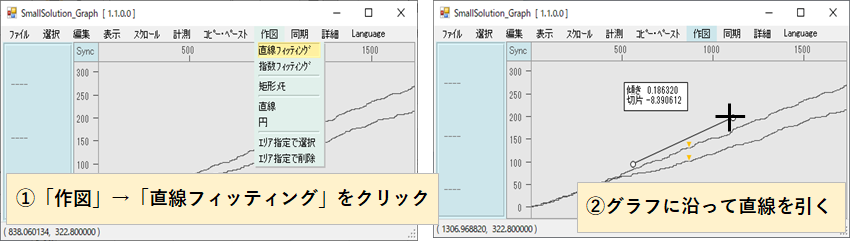
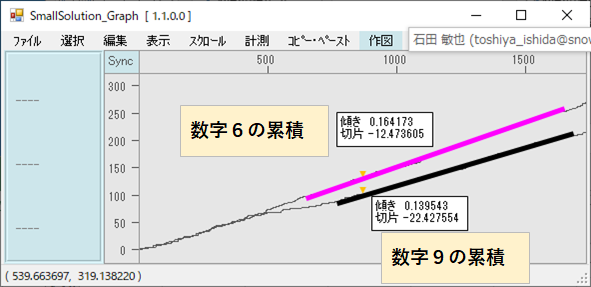
ロト６の数字６と９の累積を例に部分的に直線フィッティングしてみました。直近の傾きでは約0.139と0.164の差がついてるのが分かります。数値９は５００回目あたりで出目確率が急に落ちているのがわかります

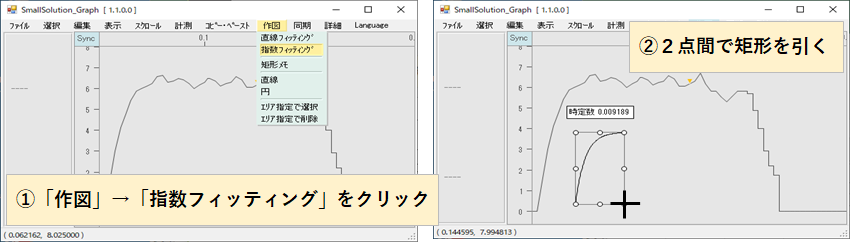
指数フィッティング

テストデータの「Transient.csv」を読込んで過渡応答の時定数を分析してみます

①「作図」→「指数フィッティング」をクリック

②２点間で矩形を作図します

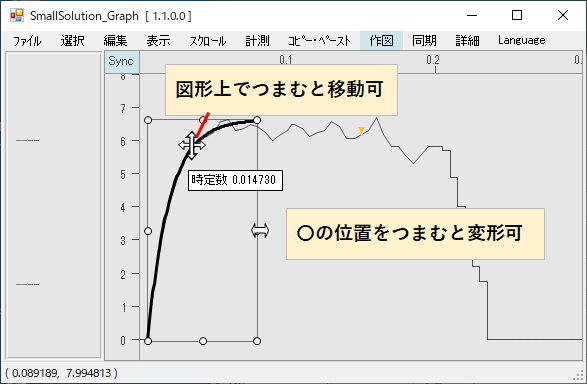
指数図形は、移動と変形ができますので下図のように近似してみると、時定14.7msが読み取れます。このデータは、DCモータの過渡応答で想定内の時定数でした

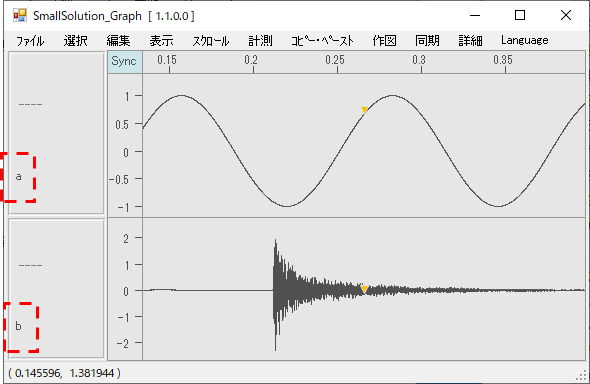
グラフ同士の四則演算

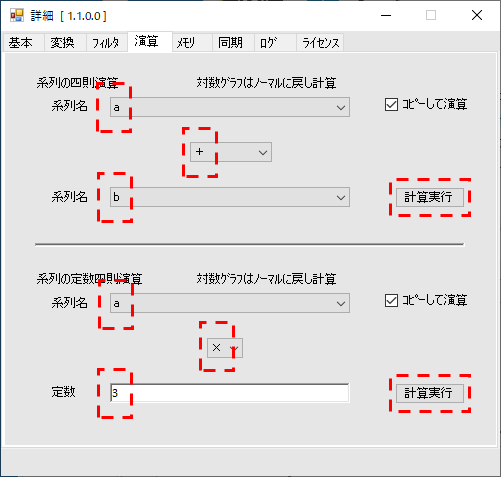
ここでは、グラフ同士の足算と、グラフと定数の乗算を説明します

テストデータ「Sin.csv」と「Can.csv」を読込みます。タイトルパネルの系列に「a」と「b」を入力します。マウスを入力位置にもっていってクリックすれば系列欄が入力モードとなります

メニューの「詳細」から詳細パネルの演算タブを開くか、グラフ上で右クリックして「算術演算」→「四則演算」をクリックして詳細パネルの演算タブを開きます

・系列名をそれぞれ下記の通り選択し、定数は任意の値を入力します

・グラフ同士の足算にある「計算実行」をクリックすると「a+b」のグラフが現れます

・グラフと定数の乗算にある「計算実行」をクリックすると「aｘb」のグラフが現れます

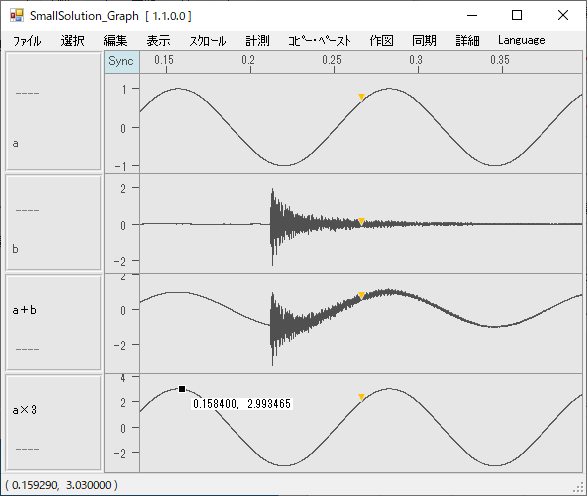
各グラフを別々の機器で測定するとサンプリング時間が異なってしまい、グラフ同士の四則演算をエクセルで行おうとしてもできません
注）グラフ同士の除算で０除算が発生した場合は、警告を出し結果は０として表示します